Jesteśmy na półmetku lata i czuć już zmęczenie słońcem i upałami. Czuć też pewne przesilenie. Dni są zdecydowanie krótsze niż na początku frenetycznego lipca. Gdzieś na horyzoncie pojawia się wizja przyjemnych październików i aż-za-zimnych listopadów. Wizja ta jest trochę nieprzyjemna, bo jej perspektywy nagle to całe wyczekiwane wakacyjne lato okazuje się że było krótkie. Ciekawe jak zmienność pór roku wpłynęła na naszą cywilizację.
W przeciwieństwie do większości znanych mi osób nie lubię spać przy zamkniętych okiennicach, toteż z ulgą konstatuję te dłuższe i chłodniejsze noce, bo oznaczają one lepszy sen. Lepszy sen, powrót wspomnień i życia wewnętrznego, które ma tendencje do zanikania kiedy spędza się wakacje na plaży.
Wspominam studia, fascynujące wykłady profesora Staruszkiewicza z mechaniki klasycznej. To chyba on wprowadził pojęcie zmiennych kanonicznych. Długo nie mogłem pojąć czemu używa się słowa 'kanoniczne' do nazwania parametrów takich jak położenie i pęd. Przeszkadzała mi oczywiście konotacja religijna: 'kanoniczne' miało, i ma, bardzo specyficzny wydźwięk. Istnieje na przykład prawo kanoniczne, z którym przecież zmienne kanoniczne nie mają nic wspólnego. Zmienne kanoniczne to kolejny przykład jak niektóre nazwy używane na przykład w fizyce konfundują studentów i utrudniają edukację. I zostają w głowie jako problem przez dziesiątki lat.
Zmienne kanoniczne to zbiór pędów i współrzędnych elementów układu fizycznego potrzebne do jego opisania w Hamiltonowskim formalizmie starej dobrej newtonowskiej mechaniki klasycznej. To pewnie nadal dość skomplikowane wyjaśnienie, spróbujmy inaczej. Przymiotnik kanoniczny oznacza formę, sposób ekspresji praw przyrody, który jest najprostszy do pojęcia. No bo można wymyślać różne skomplikowane zmienne do opisu danego systemu, ale najlepiej jest użyć zmiennych najprostszych.
W mechanice Hamiltonowskiej pęd i położenie są kanonicznie sprzężone, co oznacza że można zamienić je miejscami w równaniach Hamiltona:
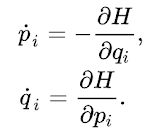
No comments:
Post a Comment